4.4.2 Tipificación de estructuras de rasgos

La evolución más interesante de este método de representación es sin duda el formalismo de estructuras de rasgos tipificadas (TFS: Typed Feature Structures), que representa un intento de sintetizar conceptos clave provenientes de los formalismos gramaticales basados en la unificación anteriormente mencionados, los lenguajes de representación del conocimiento clásicos (redes semánticas, marcos, etc.) y la programación lógica (Zajac 1992). El formalismo soporta un estilo de programación orientado al objeto basado en la abstracción y la generalización a través de la herencia. El desarrollo del concepto de tipo en relación con las estructuras de rasgos se debe principalmente a Aït-Kaci (1984, 1986), Pollard & Sag (1987), Smolka (1988, 1989), Emele & Zajac (1989, 1990) y Carpenter (1992).

Las TFSs se pueden definir matemáticamente como DAGs con raíz cuyos arcos y nodos han sido etiquetados. Sin embargo, a diferencia de éstos, una TFS puede ser cíclica (Zajac 1992). Formalmente, se puede definir una TFS como una 2-tupla <t, rasgos>, donde t Tipos, es decir, el conjunto de todos los tipos, y rasgos es el (posiblemente vacío) conjunto de rasgos.

A primera vista, la única diferencia con las estructuras de rasgos tradicionales es el etiquetado de los nodos, pero hay diferencias más profundas. Cada uno de los tipos tiene un conjunto fijo de rasgos con sus propios atributos y valores y configura el tipo de valor apropiado para un rasgo determinado. Este tipo es el supertipo más específico de todos los posibles valores para ese rasgo. De este modo, una estructura de rasgos tipificada es de hecho una instanciación de un tipo; los tipos se pueden considerar como plantillas para las estructuras y rasgos.

La repercusión inmediata en las operaciones de unificación es que al unificar dos estructuras de rasgos es necesario unificar también sus tipos. Dos tipos son unificables si son consistentes (Carpenter 1991), es decir, si tienen un subtipo común. Al igual que ocurre con las estructuras de rasgos propiamente, los tipos se organizan en una jerarquía con herencia, donde se cumple que si , decimos que subsume a , que significa que es un supertipo de o al menos es tan general como éste. Del mismo modo, decimos que extiende a , es decir, es al menos tan específico como o es un subtipo de . La Figura 4.23 muestra una jerarquía de tipos sencilla donde se da agr sing 3-s-neut.

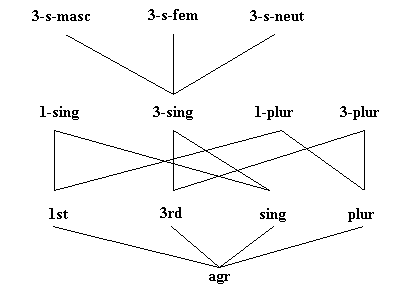
Figura 4.23 Una jerarquía de tipos sencilla

En una jerarquía de tipos existe un tipo especial denominado tipo "bottom" o tipo universal, escrito , que es el más general y por tanto subsume a todos los demás tipos de la jerarquía, es decir ={}, tal que para todo Tipo, donde {} es un conjunto consistente de tipos. En nuestro ejemplo, agr es el tipo universal de esta jerarquía, es decir, = agr.

La aplicación del concepto de tipo a las estructuras de rasgos implica la tipificación no sólo de las estructuras en sí sino también de cada uno de los rasgos.

La tipificación de los valores permite agrupar en una única estructura diferentes tipos de información (Pollard & Sag 1987). Por ejemplo, la Figura 4.24²⁹ es de tipo sign, el atributo orth tiene un valor de tipo orth (que será instanciado a la forma ortográfica de una expresión lingüística); el valor del rasgo syn es de tipo syn (que se unificará con información sintáctica de una expresión) y el rasgo sem es de tipo sem , que se refiere al contenido semántico de la expresión.

Figura 4.24 Una TFS simple

Por tanto existen dos componentes básicos en un sistema de TFS: una jerarquía de tipos y sus TFSs asociadas, estando ambos íntimamente relacionados. Los tipos no se pueden asociar libremente con cualquier FS, sino que se hallan restringidos. Cada tipo en la jerarquía debe estar asociado con una TFS, que es su restricción ("constraint").

La restricción de un tipo es una TFS de ese tipo. Por ejemplo, la restricción del tipo sign puede ser definida como la TFS de la Figura 56. Esta restricción implica que cualquier TFS de tipo sign debe contener los rasgos orth, syn y sem, con sus valores (a su vez tipificados) asociados. Es importante distinguir entre la restricción y la TFS. La primera es una definición que especifica restricciones sobre una estructura, mientras que la segunda es una instanciación de esa definición. Una estructura de rasgos bien formada (WFFS: Well Formed Feature Structure) es una TFS que satisface las restricciones de su tipo y cuyos rasgos tienen a su vez WFFSs por valores (Carpenter 1992).

El formalismo TFS soporta herencia múltiple, que se consigue mediante la reentrada. Ésta se marca en las AVMs mediante números enteros encerrados en un cuadrado. La Figura 4.25 muestra una TFS con reentrada.

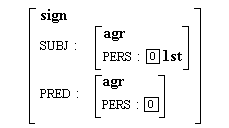
Figura 4.25 TFS con rasgos reentrantes

Esta TFS representa una regla de concordancia de persona entre sujeto y predicado mediante un rasgo reentrante. En la práctica esto se reduce a una variable dependiente que cambiará su valor según se instancie <subj pers>.³⁰

En la TFS de la Figura 57 la reentrada sirve para designar la herencia de rasgos atómicos, pero también pueden ser utilizada para señalar la herencia de TFS completas, tal y como se muestra en la Figura 4.26, donde toda la información pertinente a concordancia de persona y número del nombre es heredada por el verbo haciendo referencia una sola vez a toda la estructura <subj agr>.

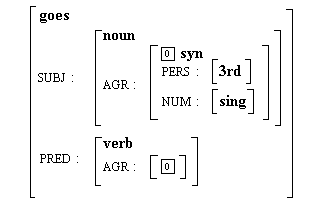
Figura 4.26 Herencia de estructura mediante reentrada

De hecho, ésta es la práctica habitual y lo obligado si se sigue una tipificación estricta (Carpenter 1991, 1992), donde incluso los valores atómicos han de ser descritos como estructuras, de ahí que hayamos cerrado entre corchetes los valores <3rd> y <singular>.

Con la tipificación se restringe el número de estructuras de rasgos "permitidas", lo que tiene como consecuencia una disminución de los elevados tiempos de proceso requeridos a los que antes hacíamos referencia. Es decir, no sólo no aumenta la complejidad de la unificación sino que para muchas aplicaciones la información de tipos reduce el tiempo empleado en computar la unificación estructural y la recursividad (Carpenter 1991; Akker et al. 1995).

Otra diferencia importante con las estructuras de rasgos sin tipificación (como por ejemplo las usadas en PATR), es que aunque éstas contienen un mecanismo de herencia simple utilizado para organizar las descripciones léxicas, una red jerárquica de TFSs posee un mecanismo de herencia más expresivo, que permite el uso de definiciones de tipo recursivas (como hemos visto en la definición de la jerarquía de tipos) y herencia múltiple. La recursividad es algo que queda fuera del alcance de las FSs puesto que éstas son expandidas estadísticamente mediante un mecanismo de macros. Además, la tipificación aporta la noción de WFFS que se utiliza para implementar una disciplina tipológica con comprobaciones de consistencia (Zajac 1992).

En el resto de este apartado describiremos algunas de las implementaciones más interesantes de este tipo de formalismos. La primera es un formalismo para la representación de las estructuras de rasgos sin tipificación y que incorpora la unificación como mecanismo expresivo fundamental. La segunda no incorpora la unificación, pero posee un tratamiento interesante del concepto de herencia múltiple por defecto no-monotónica. La tercera, la más moderna, incorpora ambos mecanismos.

NOTAS

29. Para ilustrar el formalismo TFS utilizaremos ejemplos que representan posibles fragmentos de una gramática estilo HPSG, ya que ésta ha sido hasta ahora la única teoría lingüística formal basada por completo en el formalismo TFS.
30. Los paréntesis angulares se utilizan para demarcar un camino ("path"), que se refiere a una porción determinada de una TFS (Shieber 1986).