4.4.5 ALE

ISSN: 1139-8736
Depósito Legal: B-35510-2000

4.4.5 ALE

ALE (Attribute Logic Engine) (Carpenter 1993; Carpenter & Penn 1997) constituye la implementación más importante del formalismo basado en restricciones más extendido: las estructuras de rasgos tipificadas. ALE es un sistema de representación y análisis léxico que retoma la herencia de PATR-II, con el que guarda muchas similitudes y lo mejora en muchos aspectos.

Ya vimos cómo PATR conseguía disminuir uno de los problemas inherentes a las CFGs, la sobregeneración. Sin embargo, éstas tienen un segundo problema bien conocido, que ya hemos mencionado: la arbitrariedad. Este problema sí es abordado por ALE y en general por el formalismo gramatical para el que fue diseñado, HPSG.³⁴ Otra ventaja de ALE respecto a los dos formalismos anteriores es que combina las ventajas para el proceso de PATR y la facilidad de representación de DATR. En contra, ALE presenta una orientación clara hacia un formalismo gramatical determinado, mientras que tanto PATR como DATR no son tan específicos.

A nivel de implementación, ALE también aporta grandes innovaciones. Para empezar, se trata de un compilador de gramáticas, no un intérprete. La lentitud de los lenguajes interpretados en todos los ámbitos computacionales es de sobra conocida. En el caso de los lenguajes basados en unificación, ya advertimos de este problema y apuntamos al mecanismo de tipificación como una solución. ALE hace uso de una tipificación "fuerte", que comentaremos después, pero además, la implementación está basado en la Máquina Abstracta de Warren (WAM: Warren Abstract Machine) (Aït-Kaci 1991). El desarrollo de la WAM ha conseguido hacer de Prolog un lenguaje multi-propósito con funcionalidades en cuanto a velocidad de ejecución parecidas a las de lenguajes compilados (procedimentales) tradicionales.

ALE utiliza este mismo mecanismo, con lo que teóricamente su velocidad de ejecución se equipara con la de un programa en Prolog compilado (Carpenter & Penn 1997). ALE implementa todas las características que vimos en el apartado 4.4.2, por lo que no volveremos a mostrar las operaciones básicas de subsumpción y unificación, sino que nos concentraremos en el sistema de tipificación. Lo que realmente distingue a ALE de otros enfoques basados en estructuras de rasgos es que mantiene una disciplina de tipificación "fuerte" (Carpenter 1993; Carpenter & Penn 1997). Esto significa que cada una de las estructuras de rasgos, sin excepción, ha de ser especificada con un tipo. Como ya explicamos entonces, los tipos se organizan en una jerarquía donde las restricciones sobre tipos más generales son heredadas por los subtipos. Con esto se consigue el tan deseado polimorfismo³⁵ basado en herencia. Por lo tanto, lo primero en una gramática ALE es la declaración de tipos, por ejemplo:

bot sub [b,c]. b sub [d,e]. d sub [g,h]. e sub []. c sub [d,f]. f sub [].

Los tipos declarados en esta jerarquía son bot, b, c, d, ey f. bot es un tipo especial que se declara como "top" (T), del que (en este caso) b y c son subtipos. Los tipos e y f no tienen ningún subtipo, es decir, son "bottom" (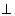). También tenemos un caso de herencia múltiple, el tipo d hereda de b y c. La Figura 4.31 muestra esta jerarquía gráficamente.

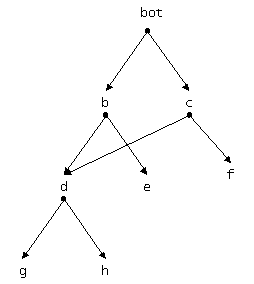
Figura 4.31

Figura 4.31 Jerarquía de tipos con herencia múltiple

La definición de la jerarquía de tipos no es todo lo que se necesita para que ALE sea caracterizado como un entorno con tipificación "fuerte". El segundo componente del sistema de tipos es el concepto de conveniencia de rasgos (feature appropriateness) (Carpenter & Penn 1997), mediante el cual cada tipo debe especificar para qué rasgos puede ser definido y además qué tipo de valores pueden tomar esos rasgos. La conveniencia también es heredada en la jerarquía, por lo que si un determinado rasgo es apropiado para un determinado tipo, también lo será para todos sus subtipos; lo mismo ocurre con los valores de los rasgos. En ALE todas las estructuras de rasgos deben respetar las restricciones de conveniencia en las declaraciones de tipo, lo que implica dos restricciones:

Si un rasgo es definido para una estructura de un tipo determinado, ese tipo debe ser apropiado para ese rasgo. Además el valor del rasgo debe ser del tipo apropiado.
De forma inversa, sin un rasgo es apropiado para un tipo, cada una de las estructuras de rasgos de ese tipo debe tener un valor para ese rasgo.

Si una estructura de rasgos respeta estas dos condiciones, se dice que está totalmente bien tipificada (totally well-typed) (Carpenter 1992). Obviamente esto es un claro esfuerzo por acabar con el problema de la arbitrariedad característico de las gramáticas de estructura de frase libres de contexto que ya hemos comentado en varias ocasiones. Mediante un sistema de tipificación como éste se consigue restringir enormemente tanto las descripciones de las entradas léxicas como las reglas sintagmáticas.

ALE corre sobre Quintus Prolog, Sicstus Prolog y SWI-Prolog. Una vez compilado en memoria, ALE acepta una serie de comandos de línea con los que se puede, entre otras cosas, compilar una gramática ALE (mediante el predicado ALE compile_gram/1). Una típica sesión de ALE comienza del modo siguiente:³⁶




Welcome to SWI-Prolog (Version 2.8.2)

Copyright (c) 1993-1997 University of Amsterdam. All rights reserved.

For help, use ?- help(Topic). or ?- apropos(Word).

1 ?- qcompile(ale203).



ALE Version 2.0.3; 1 Mar 1997

Copyright (C) 1997, Bob Carpenter and Gerald Penn

All rights reserved.



interpreter is inactive

c:/win32app/swiprolog/ale203.pl *qcompiled*, 0.33 sec, 148,980 bytes.

Yes



2 ?- compile_gram(hpsg).



   Yes

   3 ?-

A partir de este momento, el inductor de comandos será analizado, además de por el motor de Prolog, por el de ALE, por lo que podemos, por ejemplo, hacer consultas sobre las entradas léxicas incluidas en la gramática que acabamos de compilar:

4 ?- lex(book). WORD: book ENTRY: word QRETR list_quant QSTORE e_set SYNSEM synsem LOC loc CAT cat HEAD noun CASE case MOD none PRD bool MARKING unmarked SUBCAT ne_list_synsem HD synsem LOC loc CAT cat HEAD det SPEC synsem LOC loc CAT cat HEAD head MARKING marking SUBCAT list_synsem CONT sem_obj CONX conx BACKGR set_psoa C_INDS c_inds ADDRESSEE ref GEN gend NUM num PER per SPEAKER ref GEN gend NUM num PER per UTT_LOC ref GEN gend NUM num PER per NON_LOC non_loc INHERITED non_loc_1 QUE set_npro REL set_ref SLASH set_loc TO_BIND non_loc_1 QUE set_npro REL set_ref SLASH set_loc MARKING marking SUBCAT e_list CONT sem_obj CONX conx BACKGR set_psoa C_INDS c_inds ADDRESSEE ref GEN gend NUM num PER per SPEAKER ref GEN gend NUM num PER per UTT_LOC ref GEN gend NUM num PER per NON_LOC non_loc INHERITED non_loc_1 REL set_ref SLASH set_loc TO_BIND non_loc_1 TL e_list CONT npro INDEX [0] ref GEN neut NUM sing PER third RESTR ne_set_psoa ELT psoa NUCLEUS book INST [0] QUANTS e_list ELTS e_set CONX conx BACKGR e_set C_INDS c_inds ADDRESSEE ref GEN gend NUM num PER per SPEAKER ref GEN gend NUM num PER per UTT_LOC ref GEN gend NUM num PER per NON_LOC non_loc INHERITED non_loc_1 QUE e_set REL e_set SLASH e_set TO_BIND non_loc_1 QUE set_npro REL set_ref SLASH set_loc ANOTHER? n. Yes 5 ?-

La mayoría de las propiedades que muestra esta consulta son heredadas, como podemos comprobar viendo la entrada léxica real en la gramática que hemos compilado (hpsg.pl) para "book":

book ---> word, synsem:loc:(cat:(head:(noun, mod:none), subcat:[(@ detp)], marking:unmarked), cont:(npro, index:(ref,Ind, per:third, num:sing, gen:neut), restr:(elt:(nucleus:(book, inst:Ind), quants:[]), elts:e_set)), conx:backgr:e_set), (@ empty_inher), qstore:e_set.

Para no extendernos demasiado, no mostraremos el resto de las funcionalidades de ALE, aunque algunas merece la pena mencionar algunas de ellas, como su capacidad para manejar macros, o el nutrido conjunto de comandos que acepta.

Para finalizar, mencionaremos la forma en que ALE lleva a cabo el análisis sintáctico. Una consecuencia de tener a disposición dos motores de inferencia (el de ALE y el de Prolog) es que se pueden escribir dos tipos de gramáticas: de estructura de frase (ALE) y DCG (Prolog). El componente de ALE encargado de procesar las reglas de estructura de frase (o reglas sintagmáticas) es una combinación de la funcionalidad del sistema PATR-II, y la DCG de Prolog (Carpenter & Penn 1997). De hecho, ALE contiene un sistema igual al DCG con dos diferencias principales:

La DCG utiliza términos de primer orden para la representación de categorías y sus partes, mientras que ALE utiliza descripciones en forma de estructuras de rasgos soportadas por el motor lógico de atributos:valores.
La DCG de los intérpretes o compiladores Prolog codifica las gramáticas directamente como cláusulas Prolog y las evalúa de forma descendente en profundidad (top-down, depth-first). En cambio, ALE utiliza un parser de "chart" activo con análisis ascendente.

Ya hemos mostrado cómo se especifica una entrada léxica para una gramática sintagmática en ALE. El otro componente de este tipo de gramáticas es, como ya hemos visto, las reglas. ALE distingue dos tipos de reglas: léxicas y gramaticales, utilizando un formato parecido al de PATR.

Las reglas léxicas están enfocadas al tratamiento de la morfología, tanto flexiva como derivacional. El sistema de reglas léxicas de ALE es productivo, esto significa que las reglas se pueden aplicar de forma secuencial a su propio output o al output de otras reglas léxicas. Por ejemplo, podemos derivar el sustantivo "winner" a partir del verbo "win" y a continuación derivar el plural "winners" a partir del singular, y así sucesivamente.

Además se pueden especificar límites en la profundidad de aplicación de reglas que se permite alcanzar. La descripción de la sintaxis concreta para la especificación de reglas léxicas se encuentra en Carpenter & Penn (1997).

Finalmente, las reglas gramaticales de ALE son por supuesto del tipo de PATR, es decir, reglas sintagmáticas de reescritura.³⁷

Nos hemos detenido a analizar con alguna profundidad este entorno, ya que, aunque no lo utilizaremos para nuestra implementación, mantiene muchos puntos en común con el sistema de marcos que mostraremos en el siguiente capítulo para implementar la ontología.

El paralelismo entre un entorno como ALE y un sistema de redes semánticas basado en marcos no es accidental. De hecho, ALE pretende implementar algunas de las características más sobresalientes de estos esquemas de representación y aplicarlas exclusivamente a la representación de información léxica.

El entorno que utilizaremos para el desarrollo de nuestra ontología, FLEX, carece de la imposición de restricciones que el entorno ALE ofrece, así como del mecanismo de unificación, pero a cambio ofrece otras muchas características enfocadas al desarrollo de aplicaciones de carácter general e implementa todas las características deseables en un entorno basado en marcos. Además, también ofrece todas las posibilidades del sistema Prolog sobre el que corre y que le sirve de motor lógico. En el siguiente capítulo describiremos todas estas características en detalle.

NOTAS

La mayor parte del trabajo realizado con ALE has sido en el seno de la HPSG, sin embargo, también se han escrito gramáticas basadas en GPSG y CG.
El término polimorfismo se toma de los lenguajes orientados al objeto para designar la característica de estos lenguajes que permite implementar múltiples formas de un mismo método, dependiendo cada una de ellas de la clase sobre la que se realice la implementación. Esto permite acceder a una variedad de métodos distintos (todos con el mismo nombre) utilizando exactamente el mismo medio de acceso (Ceballos 1993).
Este ejemplo corresponde al output de ALE 2.0.3 ejecutándose bajo SWI-Prolog 2.8.2 en plataforma Win32.
Como se puede observar en la entrada léxica que hemos mostrado ("book"), también las entradas léxicas se especifican mediante el formato clásico de reescritura.

Anterior I Siguiente I Índice capítulo 4 I Índice General