ISSN:
Depósito Legal:
6.7.3. Meronimia y transitividad
El problema de la transitividad en las meronimias ha sido el más estudiado (ver capítulo 2). No vamos a retomar todos los argumentos que ya se han expuesto anteriormente, sino que vamos a intentar analizar la propiedad desde el punto de vista del modelo relacional que estamos utilizando. Así, la transitividad se convierte en una relación derivada a partir de dos relaciones no derivadas.
R(A,B) R(B,C) R(A,C)
Pero la transitividad puede expresarse formalmente, además de en términos relacionales, en términos de teoría de conjuntos:
A B y B C A C
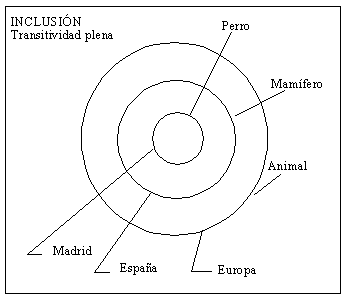
Cuando hablamos de inclusión, la transitividad se cumple en todos los casos. Ahora bien, con respecto a las meronimias hay distintos aspectos que tenemos que considerar antes de intentar comprobar si es o no es transitiva y en qué condiciones.
El primer aspecto trata de algo comúnmente aceptado: existe un problema con las propiedades booleanas cuando afectan a entidades de distinto tipo (como un elemento y un conjunto). Efectivamente, si hablamos de pertenencia ( ) de elementos a conjuntos y de inclusión ( ) entre conjuntos (como puede considerarse en la relación meronímica tornillo-cerradura-puerta-casa) deberemos tener en cuenta este problema.
Muchas veces podemos considerar, además, en el uso normal del lenguaje, unidades que son conjuntos como si fueran elementos. Por ejemplo, normalmente no consideraremos «picaporte» como un conjunto, a no ser que seamos especialistas o fabricantes de picaportes o lógicos y pensemos en el conjunto de todos los picaportes, sino como un elemento. En este sentido, existe una diferencia entre el uso lingüístico y la realidad, pues físicamente un picaporte es parte de una casa, en cambio la oración el picaporte es parte de la casa no es válida. A menudo estamos manejando dos entidades diferentes: elementos y conjuntos.
Por otro lado, en 1965, Zadeh introdujo la idea de conjuntos difusos, precisamente para tratar aquellas colecciones cuyas propiedades de pertenencia (miembros) no estaban claramente definidas.
Por último, si consideramos todos los significados que intervienen en una meronimia como conjuntos, para así evitar el problema expuesto en primer lugar, y esgrimimos la coincidencia de propiedades, atributos y relaciones de cada significado para ver si unos están incluidos en otros (y poder aplicar así la transitividad canónica), nos daremos cuenta de que en muchos casos no existe inclusión (como en la hiponimia), sino intersección. Es decir, a diferencia de la hiponimia, en la que los nodos descendientes heredan TODAS las propiedades de los nodos ancestros, es decir, están incluidos en ellos, como en el primer gráfico, en la meronimia hemos visto que no es así. Es decir, un merónimo y su holónimo pueden compartir todas, algunas o ninguna propiedad. Esto podría representarse como en el segundo gráfico, en el que lo que hay es una intersección.
Si la relación es de pertenencia y la transitividad es por inclusión: Si a A y A B, entonces a B.

Si la relación es de pertenencia y la (no) transitividad por intersección: Si a A y A B, entonces a B si a (A B) y a B si a (A B).
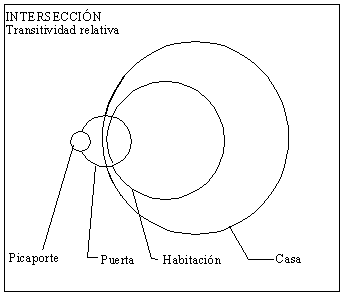
Creemos que considerar estos tres aspectos podría contribuir al esclarecimiento del problema de la transitividad en las meronimias, como muestra gráficamente la segunda representación. Ambos planteamientos explicarían además por qué algunos subtipos de meronimias parecer ser SIEMPRE transitivos, el que combina pertenencia e inclusión, y otros, en cambio, a veces lo son y otras no, el que combina pertenencia e intersección. Sin embargo, necesitamos una explicación que dé fundamento a esta concepción y representación y que permita además ser aplicada coherente y sistemáticamente.
No obstante, una primera inspección de los subtipos meronímicos, a la luz de esta diferenciación entre transitividad plena o inclusión y transitividad relativa o intersección, podría ser la siguiente:
| Subtipo de meronimia | Ejemplos | Transitividad plena (inclusión) | Transitividad relativa (intersección) |
| componente-objeto (holo-1, mero-1) |
picaporte-puerta-casa uña-mano-brazo |
- | + |
| miembro-colección (holo-2, mero-2) |
uva-racima-racimo | + | - |
| porción-masa (holo-3, mero-3) |
milímetro-centímetro-metro | + | - |
| materia-objeto (holo-4, mero-4) |
alcohol-vino-sangría | + | - |
| acción-actividad (holo-5, mero-5) |
imagen-secuencia-escena momento-culminación-situación |
+ | - |
| lugar-área (holo-6, mero-6) |
localidad-provincia-región | + | - |
| relación genérica (holo-0, mero-0) |
solapa-pieza-ensambladura | + | - |
| relación por ausencia | holo-absentia, mero-absentia | No es aplicable | No es aplicable |
De entre los datos que hemos recogido, a veces la falta de transitividad es evidente, como en:
aguapié : Vino muy flojo sacado echando agua en el orujo después de haberlo exprimido.
En este ejemplo tenemos que aguapié >mero-4> orujo, agua; agua >mero-4> oxígeno. Difícilmente podemos decir que el oxígeno forma parte del aguapié, sin tener un contexto muy específico. Además, pueden crearse circularidades motivadas o correctas, como en este caso, en la que el agua es parte del grupo meronímico en más de una ocasión:
aguapié >mero-4> agua @ orujo > mero-4 > agua
A menudo la transitividad es utilizada en las definiciones para desambiguar o individualizar el significado o para ampliar información. Este uso explícito de la transitividad es sin embargo ad hoc. El siguiente caso muestra el encadenamiento de dos meronimias de distinto tipo, entre las que hay una transitividad explícita (metalla > mero-2 > trozo-#1 > mero-4 > oro-#1), ya que no sólo es válido, sino además necesario, inferir que la medalla es de oro.
metalla-#1|Sustantivo|clase|import|general|conjunto-#1|holo-||mero-2|trozo-#1>oro-#1|sinónimo|
|dorado@adorno|Colectivo genérico. Trozos pequeños de oro que usan los doradores para completar el dorado en las partes que han quedado descubiertas1.polo-#1|Sustantivo|clase|import|general|extremo-#1|holo-6|eje-#1|holo-1|curva-#1@esfera-#1|sinónimo|
|curva@esfera|Cada extremo del eje de una curva o una esfera.
Existe pues un uso discriminado de la transitividad que invalida la afirmación de Chaffin, Hermann y Winston (1988) que dice que no se cumple la transitividad si se intenta hacer a través de dos subtipos meronímicos distintos. Según esta observación tendríamos tanto línea meronímica típica transitiva como línea meronímica no-típica transitiva. Sin embargo, creemos que la segunda sólo se cumple en casos muy concretos.
En este ejemplo la representación es incompleta y errónea si no añadimos un nivel más en la representación de la meronimia.
punto-#4|Sustantivo|clase|import|general|parte-#1|holo-1|punta-#1>pluma-#2|mero-|
|sinónimo||pluma@utensilio@escritura|Cada una de las partes en que se divide la punta de la pluma de escribir.
También podemos considerar el siguiente ejemplo de meronimia miembro-colección como poseedora de tres niveles de meronimia, lo cual no es nada común, e incluso transitiva: racima->racimo->uva
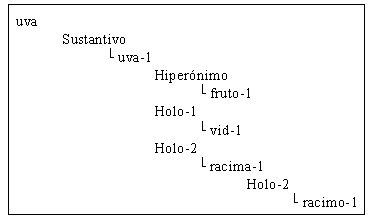
racima-#1|Sustantivo|clase|import|general|conjunto-#1|holo-||mero-2|racimo-#1|sinónimo||vendimia@agricultura|Conjunto de racimos pequeños que quedan en las vides después de la vendimia.
Este hecho, aunque pueda parecer extraño, no lo es tanto, pues algunos nombres colectivos especializados necesitan dos niveles de holónimos para ser correctamente individualizados: conjunto > grano > uva.
racimo-#1|Sustantivo|clase|import|general|conjunto-#1|holo-||mero-2|grano-#1>uva-#1|sinónimo||planta|Conjunto de granos de uva sostenidos en un mismo tallo.
Hemos visto que algunas definiciones contienen hasta dos y tres niveles de relaciones meronímicas, pero normalmente de merónimo a holónimo (tiene_holónimo_), y no al revés. Sin embargo, en el siguiente caso sí:
sacabotas-#1|Sustantivo|clase|import|general|utensilio-#1|holo-||mero-1|tabla-#1>muesca-#1|sinónimo|
|utensilio|Utensilio formado por una tabla con una muesca en la que se introduce el tacón de la bota, por ejemplo de las altas de los militares, para sacársela.
El siguiente ejemplo, en cambio, necesita una descripción meronímica de hasta cuatro niveles:
zanco-#2|Sustantivo|clase|import|general|parte-#1|holo-1|faldón-#1>armadura-#1>tejado-#1>|mero-|
|sinónimo||faldón@casa|Parte inferior del faldón de una armadura de tejado.
Como podemos ver, no sólo existe la transitividad en las meronimias sino que a veces es el mecanismo fundamental por el que podemos desambiguar o individualizar el significado. Aquí, manga es parte del eje, pero no del eje de una noria, sino del eje de un carruaje. Ante este caso, deberíamos crear dos unidades semánticas distintas, una para el primer eje y otra para el segundo, o bien debemos considerar una condición o propiedad adherida a la relación concreta a la que afectan. Como fenómeno local, que sólo afecta a esa relación, sería poco práctico crear registros o unidades semánticas distintas para estos casos, ya que estaríamos acercándonos a una base de conocimiento no sólo léxico, ya que estos casos no están lexicalizados (como por ejemplo caña-#5, hipónimo de eje-#1, que es el eje de un «ancla»).
| <Entrada> (26) <Synset> : manga-#5, mangueta <Atributos> <Categoría> : Sustantivo <Tipo> : Clase <Léxico> : General <Glosa> : Parte del eje de un carruaje en que gira la rueda. <Relaciones> <Relaciones de Clase> <Clave semántica> : eje, carruaje <Hiperónimo> : parte-#1 <Relaciones de Holonimia> <Holonimia Tipo> : holo-1 <Holónimo> : eje-#1 <Holonimia Tipo> : holo-1 <SubHolónimo> : carruaje-#1 |
A pesar de las excepciones que hemos encontrado a la generalización sobre la transitividad en las meronimias de Chaffin, Hermann y Winston (1988), hemos encontrado un indicio de generalización que se encuadra en la misma línea de sus observaciones, pero no desde el punto de vista del tipo de relación, sino desde el punto de vista del tipo de significados relacionados. La generalización sería la siguiente:
Existe transitividad si los significados involucrados en las dos premisas son co-hipónimos directa o indirectamente entre sí, esto es, tienen el mismo anclaje semántico.
Esta generalización nos lleva de nuevo al Modelo Relacional de Anclajes. Como dijimos en un principio, los anclajes nos permiten generalizar al extrapolar las relaciones, relativas, de su entorno local a un entorno global, absolutas. Esta generalización es compatible con la visión matemática mostrada más arriba, ya que al ser co-hipónimos directos o indirectos compartirán más rasgos y por tanto habrá una amplia intersección e incluso una inclusión.
De todas formas, no podemos resolver aquí el problema de la transitividad en las meronimias, pues requeriría una investigación exclusivamente dedicada a ella. Sin embargo esperamos haber aportado algunos datos y algunas nuevas ideas para su estudio y tratamiento.
Por último, queremos llamar la atención brevemente sobre la reflexividad. Parece algo trivial hablar de reflexividad, al igual que de transitividad, en la relación de hiponimia, ya que cualquier significado ES un tipo de sí mismo (ya vimos que en el caso del orden parcial finito es un axioma). ¿Pero qué ocurre en la meronimia? ¿Todos los significados con relaciones meronímicas (recordemos que hay otros muchos SIN relaciones meronímicas) son parte de sí mismos, aunque sea en su totalidad, como ocurre con la identidad en la hiponimia? Existen casos explícitos de reflexividad en las definiciones? Si es así, ¿en qué podría diferenciarse la reflexividad axiomática de la reflexividad explícita?
Aquí, vamos a responder que NO a la primera cuestión, ya que no parece aceptable la afirmación motor es parte del motor o Europa es parte de Europa, a no ser que se trate de acepciones distintas de ‘motor’ y ‘Europa’ y las primeras sean efectivamente parte de las segundas. En cuanto a la segunda cuestión, diremos que la reflexividad explícita en una definición con respecto a la meronimia suele implicar un cambio en el valor de alguna propiedad, es decir, si parcela es parte de parcela es que la primera es menor que la segunda.
NOTAS
1 Se podría representar una meronimia que exija tres niveles de representación fraccionada en dos tipos distintos de holónimos:
polo-#1|Sustantivo|clase|import|general|extremo-#1|holo-6|eje-#1|holo-1|curva-#1@esfera-#1|sinónimo||curva@esfera|Cada extremo del eje de una curva o una esfera.
Anterior I Siguiente I Índice capítulo 6 I Índice General
ISSN:
Depósito Legal: