5.1 Módulo Gramatical para N-gramas

El diseño del Módulo Gramatical para gramáticas N-gramas está basado en el hecho de que cualquiera de ellas puede modelarse como un autómata de estados finitos, en el que los estados dependen de las restricciones que se intenten modelar con dicha gramática y su repercusión en el espacio de estados donde el Módulo Acústico buscará la solución o soluciones. En el caso más general que es el de un autómata finito representando las restricciones de la gramática, cada estado estará asociado a una categoría, y existirán tantos estados como tenga la gramática (autómata). Sin embargo, para gramáticas estocásticas de orden menor (bigramas, trigramas), el número de estados no será tan elevado pues las restricciones modeladas no serán de distancias tan largas y no habrá tantas transiciones entre estados a guardar. En la práctica, no se suelen utilizar autómatas para modelar las restricciones sintácticas del lenguaje al ser necesarios un elevado número de estados si deseamos que la cobertura de nuestra gramática sea suficiente. Suelen utilizarse gramáticas bigramas o trigramas de categorías, aunque el número de datos de entrenamiento necesario crece al aumentar el orden N de la misma como ya hemos visto.

La regla para conocer el número de estados de nuestra gramática es la siguiente: para bigramas, será V el número de estados si es V el número de categorías diferentes, y el número máximo de transiciones (restricciones) entre esos estados será VxV (tamaño máximo de la tabla de transiciones del autómata equivalente); para trigramas, será VxV el número de estados si es V el número de categorías diferentes, y VxVxV el tamaño de la tabla de transiciones del autómata equivalente. Cabe pensar que no todas esas transiciones son posibles en una lengua, hecho que es cierto, y que, por tanto, no serán tantos los datos a guardar y procesar, sin embargo, en la práctica, y para compensar conjuntos limitados de datos de entrenamiento de las gramáticas, se utilizan técnicas de suavizamiento, que intentan aumentar la cobertura de las mismas pero su coste es que la mayoría de las transiciones no observadas, incluso muchas que no serían posibles en la realidad, ahora aparecen como posibles aunque tengan una baja probabilidad de aparecer.

Veamos ahora cómo debe ser compilada la información de una gramática para que sea procesable por el Módulo Gramatical. Toda ella será almacenada en un conjunto de ficheros que leerá dicho módulo y utilizará adecuadamente para guiar el proceso de decodificación acústica que lleva a cabo el Módulo Acústico. Los ficheros de datos gramaticales serán:

• Tabla de las Transiciones entre los Estados Directa (*.TAB) e Inversa (*.INV). Es un fichero con la tabla de transiciones entre los estados de la gramática. Dependiendo del tipo de espacio de estados utilizado, puede ser necesario utilizar sólo la tabla de transiciones invertida, es decir, aquella que indica cómo se puede llegar a cada uno de los estados de la gramática desde el resto de los estados, como ocurre con los sistemas con espacios de estados estáticos, o bien ambas, en el caso de sistemas con espacios de estados dinámicos. Ya veremos esto más adelante con algo más de detalle.
• Tabla con las Probabilidades de las Transiciones entre Estados Directa (*.PRB) e Inversa (*.PRI). Este fichero tiene un aspecto similar a la Tabla de Transiciones, pero ahora cada elemento no representa un posible estado al que se puede transitar sino la probabilidad de transitar a ese estado. Complementa a la Tabla de Transiciones incorporando las probabilidades del modelo gramatical en el sistema. Existe una versión directa y otra inversa, pues debe existir coherencia con la información de la Tabla de Transiciones.
• Tabla de Estados (*.EST). Es una lista con los estados que son necesarios para representar todas las restricciones de la gramática en forma de autómata de estados finitos. Debe tenerse en cuenta que siempre deben existir 3 estados especiales cuyas categorías serán: NODOINICIAL (estado 1), NODOFINAL (estado penúltimo), y SILENCIOS (último estado). Aunque no es necesario mantener este orden puede ser conveniente para mayor claridad en la representación de la gramática. Los estados NODOINICIAL y NODOFINAL, son dos estados ficticios que permiten modelar las transiciones del principio y de final de las frases, es decir, aquellas categorías que pueden ser comienzo de frase y las que pueden finalizar una frase, según la gramática. El estado cuya categoría es SILENCIOS no va a aparecer en la Tabla de Transiciones entre Estados ya que el SILENCIO es un fenómeno puramente acústico, en el sentido de que difícilmente va a aparecer como el resto de categorías en los corpus de texto etiquetados utilizados para entrenar las matrices gramaticales. Sin embargo, debe ser incorporada en el espacio de estados convenientemente, como si se tratase de una palabra más del diccionario.
• Tabla con las Categorías de los Estados (*.CAT). Es una lista con la categoría asociada a cada estado de nuestra gramática. Debemos tener en cuenta que, en el caso de un bigrama o de un autómata finito de categorías, cada estado tiene una categoría sencilla pero en los trigramas, cada estado representa un par de categorías, pues los estados deben representar restricciones cuya historia debe considerar 2 categorías anteriores a la categoría actual. Es decir, se modelan las posibilidades de que se produzca una determinada categoría si antes se ha producido un par de categorías (en ese orden). Todo ello puede ser tenido en cuenta con el conjunto de ficheros diseñado, sin necesidad de modificar el Módulo Gramatical cuando cambiamos de gramática.

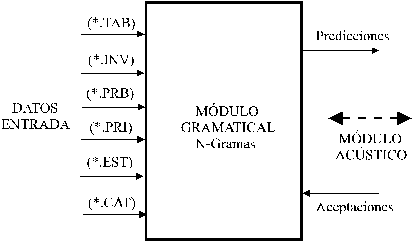
Fig.5.2 Módulo Gramatical para gramáticas N-gramas. Datos de Entrada y de Salida.

Veamos un ejemplo sencillo de un bigrama de categorías, para comprender lo fácil que es incorporar la información gramatical en el sistema:

Bigrama de Categorías

Supongamos que nuestra matriz cuadrada de pares de categorías obtenida automáticamente a partir de textos de entrenamiento debidamente etiquetados es la siguiente:

siendo las categorías: NODOINICIAL (Fila 1), C1 (Fila 2), C2 (Fila 3), C3 (Fila 4), C4 (Fila 5), NODOFINAL (Fila 6). Usamos la notación C_i pues se trata de una gramática donde lo que sea cada categoría no es relevante. En la matriz observamos las probabilidades de transitar desde cada categoría a cualquier otra, existiendo casos de probabilidad nula (0.0) que indican que esas transiciones no están permitidas. Debe suponerse que esta matriz no está suavizada pues en ese caso se permitirían, aunque con probabilidades muy pequeñas, todas las transiciones para evitar el efecto que la escasez de datos de entrenamiento tendría sobre la cobertura de la gramática. Esta matriz también nos aporta la información necesaria para la Tabla de Probabilidades de Transición además de para la propia Tabla de Transición entre Estados.

Tabla de Transiciones (EJ1.TAB)

2 3 4 5

2 3 4 5 6

2 4 5

2 3 5 6

3 5 6

Tabla de Transiciones Inversa (EJ1.INV)

1 2 3 4

1 2 4 5

1 2 3

1 2 3 4 5

2 4 5

Tabla de Probab. Inversa (EJ1.PRI)

0.2 0.1 0.3 0.2

0.4 0.3 0.3 0.3

0.3 0.2 0.2

0.1 0.2 0.5 0.1 0.6

0.2 0.4 0.1

Tabla de Probab. (EJ1.PRB)

0.2 0.4 0.3 0.1

0.1 0.3 0.2 0.2 0.2

0.3 0.2 0.5

0.2 0.3 0.1 0.4

0.3 0.6 0.1

Tabla de Categorías (EJ1.CAT)

NODOINICIAL

C1

C2

C3

C4

NODOFINAL

SILENCIOS

Tabla de Estados (EJ1.EST)
1
2
3
4
5
6
7

En la figura 5.3 podemos ver el autómata de estados finitos equivalente a ese bigrama de categorías, con el detalle de las transiciones y sus probabilidades para el estado NODOINICIAL y el estado de categoría C1.

Fig. 5.3 Autómata Finito equivalente al bigrama del ejemplo (transiciones representadas parcialmente)

Trigrama de Categorías

En el Apéndice 5.1 incluimos un sencillo ejemplo de una gramática 3-grama de categorías que nos muestra cómo es posible transformar cualquier gramática N-grama en un autómata. Sólo es necesario determinar el espacio de estados asociado a la misma, es decir, el número de copias de cada categoría y las transiciones (restricciones gramaticales) que existen entre los estados. Podemos observar cómo el diseño del Módulo Gramatical de nuestro sistema permite incorporar gramáticas N-gramas de cualquier orden, compilando la información en los distintos ficheros de información de entrada al mismo. Se comprueba cómo ha aumentado el número de estados con respecto a la gramática de orden dos (bigrama) y el número de transiciones posibles.

Anterior   I  Siguiente   I  Índice capítulo 5   I   Índice General