5.3.2.3 Estimación de los Umbrales de Recorte: Método basado en un Histograma de Distancias de los Estados de los Caminos Óptimos de las Frases de Entrenamiento y en un Factor de Conservación

Para encontrar la correlación que mencionábamos en el apartado anterior se calcularán dos histogramas de distancias:

• Histograma con la distribución de las diferencias entre las distancias de cada uno de los estados del espacio de búsqueda y la distancia del estado de menor distancia (mejor estado) en cada trama. Esa distribución de diferencias de distancias contemplará todas las tramas de cada una de las frases del conjunto de entrenamiento del sistema de reconocimiento. Por tanto, observaremos el comportamiento medio del espacio de búsqueda para un locutor.
• Histograma con la distribución de las diferencias entre las distancias de los estados de los caminos óptimos de cada una de las frases y la distancia del estado de menor distancia. Para calcular este histograma se obtendrá el conjunto de estados del camino óptimo de cada frase a posteriori, es decir, después del proceso de reconocimiento y las distancias acumuladas en la trama correspondiente para cada uno de ellos. Incluso, se diferenciarán los últimos estados de un modelo de Markov del resto de los estados del modelo en el cálculo de esas distribuciones.

Basándonos en estos histogramas podremos saber, en promedio, cuántos estados del espacio de búsqueda general y cuántos estados de los caminos óptimos de las frases se procesarán cuando apliquemos un umbral de poda. Recuérdese que el umbral de poda es un umbral de distancia calculado sumando a la distancia del estado mejor (de menor distancia) una constante. Por tanto, el umbral de recorte decidirá las bandas del histograma que se procesarán (cada banda contiene los estados cuya diferencia de distancia se encuentra entre los límites de la misma), dando lugar a un factor de conservación (el % de los estados de los caminos óptimos que se procesarán al no ser eliminados por rl umbral de recorte).

El histograma de distancias de todos los espacios del espacio de búsqueda incluye la distribución de distancias de los estados de los caminos óptimos de todas las frases del corpus de entrenamiento. Al aplicar un umbral de poda sobre el histograma de distancias de todos los estados podemos conocer el número medio de estados  que se procesarán en cada trama (coste computacional en cada trama). Si aplicamos este mismo umbral sobre el histograma de distancias de los estados de los caminos óptimos obtendremos el número de estados de los caminos óptimos que se procesarán en cada trama. Es este segundo conjunto el que determina la Tasa de Aciertos de Palabras del reconocedor. Por tanto, será el factor de conservación o número de estados de los caminos óptimos a procesar, el parámetro a correlar con la Tasa de Aciertos de Palabra del sistema. Además, el umbral de recorte aplicado sobre el histograma global (el de todos los estados) nos indicará el coste computacional efectivo.

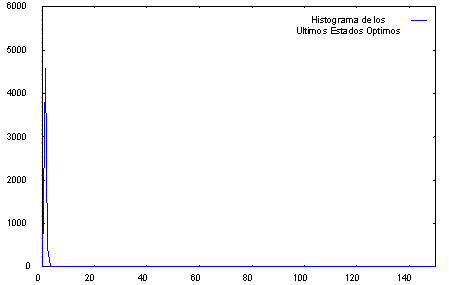
Fig. 5.11 Histograma de distancias de los últimos estados del camino óptimo para todas las frases de entrenamiento de un locutor

En la figuras 5.11 y 5.12 podemos observar los histogramas que antes comentamos, mostrando cómo se distribuyen las distancias de los estados de los caminos óptimos de las frases de entrenamiento. Se diferencian los últimos estados de cada modelo HMM de palabra del resto de los estados del modelo.

En el eje x podemos observar las distintas bandas. Cada banda establece una franja de distancias con relación a la distancia del estado de menor distancia en cada trama El eje y representa el número de estados de los caminos óptimos de todas las frases de entrenamiento cuya distancia se encuentra en cada una de las bandas.

Es importante destacar el hecho de que el número de bandas establecido afectará a la resolución del proceso. Cuantas menos bandas tengamos, mayor será cada una de ellas, y más estados contendrán cada una de ellas. De ese modo, al aplicar un umbral, para procesar un determinado número de estados de los caminos óptimos (factor de conservación), estaremos determinando qué bandas se tienen que procesar (cada banda aportará una cantidad de estados). Si las bandas son muy anchas albergarán también muchos estados que no pertenecen a los caminos óptimos y que incrementarán el espacio de búsqueda activo y por tanto, el coste computacional.

Es importante por ello, llegar a un compromiso en cuanto al ancho de cada una de las bandas del histograma. De ese modo, podremos afinar con el valor del umbral y reducir el coste computacional global.

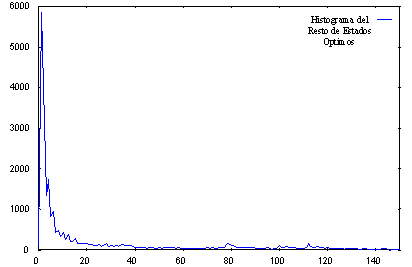
Fig. 5.12 Histograma de distancias de los estados no últimos del camino óptimo para todas las frases de entrenamiento de un locutor

Este razonamiento se entenderá mejor si se observan los histogramas de las gráficas 5.11 y 5.12 que se incluyen. La mayoría de los estados de los caminos óptimos se agrupan en la primera de las bandas, la más cercana al eje y. Si esta banda es muy ancha entrarán casi todos los estados de los caminos óptimos y será muy difícil jugar con el factor de conservación de los mismos, pero además, en esa banda entrarán muchos más estados que no son de los caminos óptimos y que realmente son los que afectan directamente al coste computacional en el sistema.

Una vez calculados los histogramas, podremos obtener, para los diferentes valores del factor de conservación que queramos considerar o estudiar, la constante a sumar al parámetro calculado en cada trama para determinar el umbral de recorte.

En la tabla 5.10 podemos encontrar los valores obtenidos para la constante a sumar en función de distintos factores de conservación. Estos resultados han sido obtenidos utilizando los datos (frases) del corpus de entrenamiento, considerando un solo umbral o dos umbrales de recorte a aplicar. En este caso no se utilizó información gramatical y los modelos de Markov utilizados son de baja calidad.

Datos de Entrenamiento – Sin Gramática

D2, NG, D-S PROMEDIO Trama Actual Espacio Tot: 31374 est.	ANCHO DE HAZ CONSTANTE Distancia a sumar a la Distancia Mínima (Margen)
	2 Umbrales		1 Umbral
Factor de Conservación	Resto Estados	Últimos Estados	Todos los Estados
100.0 %	300000	300000	300000
99.99 %	262200	163500	260400
99.90 %	222000	132900	217800
99.70 %	199800	113700	197250
99.50 %	189750	104700	186900
99.40 %	186150	100800	182850
99.30 %	182700	97950	179850
99.20 %	180150	95550	176700
99.10 %	177300	93600	173850
99.00 %	174750	91950	171450
98.50 %	165150	84300	161850
98.30 %	162300	82350	159000
98.00 %	158550	79650	154950
97.50 %	153000	75750	149550

Tabla 5.11 Umbrales Promedio para la estrategia de recorte implementada (Ancho de Haz Constante), con un sólo umbral o dos umbrales de recorte (Locutores: ENR, FER, LEA, ROM - Modelos D2 de Markov - Sin gramática - Diccionario D-S). Los umbrales han sido calculados utilizando los datos de entrenamiento.

La primera pregunta que surge está relacionada con la validez de las constantes obtenidas para los diferentes factores de conservación cuando los datos no son los de entrenamiento sino los de evaluación. Se plantea la generalidad de los umbrales de recorte que se van a obtener al sumar las constantes al parámetro calculado en cada trama cuando los datos no hayan sido observados en el cálculo de los histogramas.

Para intentar responder a esa pregunta, calculamos los mismos histogramas, manteniendo las mismas condiciones, pero ahora utilizando los datos de evaluación. Los resultados obtenidos se encuentran en la tabla 5.11, donde se pueden ver los valores de las constantes para los mismos factores de conservación, considerando uno y dos umbrales de recorte.

Datos de Evaluación - Sin gramática

D2, NG, D-S PROMEDIO Trama Actual Espacio Tot: 31374 est.	ANCHO DEL HAZ CONSTANTE Distancia a sumar a la Distancia Mínima (Margen)
	2 Umbrales		1 Umbral
Factor de Conservación	Resto Estados	Últimos Estados	Todos los Estados
100.0 %	300000	300000	300000
99.99 %	227100	161000	216584
99.90 %	194350	115150	192400
99.70 %	177700	97500	175500
99.50 %	168150	91450	165400
99.40 %	164200	89250	161350
99.30 %	161000	85350	158500
99.20 %	158500	83150	155900
99.10 %	156250	80800	153200
99.00 %	153950	78350	150600
98.50 %	144100	72600	140900
98.30 %	141350	70150	138000
98.00 %	137400	67600	134150
97.50 %	131900	63250	128750

Tabla 5.12 Umbrales Promedio para la estrategia de recorte implementada (Ancho de Haz Constante), con un sólo umbral o dos umbrales de recorte (Locutores: ENR, FER, LEA, ROM - Modelos D2 de Markov - Sin gramática - Diccionario D-S). Los umbrales han sido calculados utilizando los datos de evaluación.

Para poder ver con mayor claridad que en las tablas 5.10 y 5.11 la relación entre las constantes calculadas con los datos de entrenamiento y de evaluación, se incluye la gráfica de la figura 5.13, donde se muestra la evolución de los umbrales para los datos de entrenamiento y de reconocimiento en función de los factores de conservación.

Puede observarse que la evolución de las dos curvas es similar, por lo que a partir de ahora, y en aras de reducir tiempo de experimentación trabajaremos exclusivamente con constantes obtenidas de los datos de evaluación. Posteriormente veremos que pueden utilizarse los datos de entrenamiento para obtener conclusiones sobre las constantes a utilizar y las tasas de reconocimiento que se esperan obtener.

Si se observan los puntos A,B ,C y D podemos deducir que los umbrales de recorte calculados con las constantes obtenidas utilizando los datos de entrenamiento son claramente conservadores. Ello es debido a que la dispersión de las distancias de los estados del espacio de búsqueda es mayor al existir un mayor número de datos (el conjunto de datos de entrenamiento es 6 veces mayor que el conjunto de evaluación).

Por tanto, si utilizamos los umbrales de recorte calculados con los datos de entrenamiento para experimentar con los datos de evaluación, obtendremos Tasas de Acierto de Palabras (WA) mayores al mismo tiempo que índices de eficiencia menores.

La causa de ello es que los umbrales de recorte aplicados son mayores que los expresamente calculados con los datos de evaluación (más adaptados), recortando menos el espacio de búsqueda.

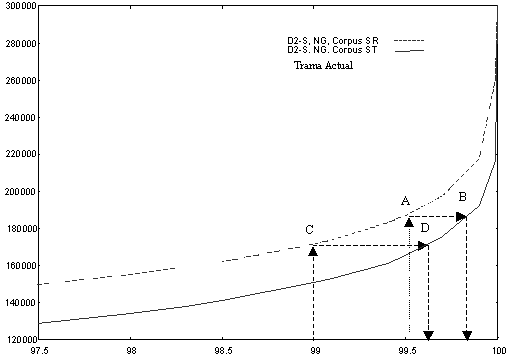
Fig. 5.13 Evolución del valor de las constantes de recorte calculadas para distintos factores de conservación, tanto para histogramas calculados con los datos de entrenamiento (corpus SR) como los calculados con los datos de evaluación (corpus ST).

Conviene destacar las diferencias entre los puntos A y C de las curvas de la figura 5.13. Se observa que a mayor factor de conservación el valor de la constante calculada con los datos de entrenamiento y utilizada en los experimentos de evaluación conduce a factores de conservación más cercanos al fijado con los datos de entrenamiento. Esto nos indica que el recorte del espacio de búsqueda conseguido con los umbrales calculados con los datos de entrenamiento será bastante menor en los experimentos de evaluación a medida que el factor de conservación disminuye, y por tanto, los umbrales calculados, aunque utilizables por conservadores, no serán eficientes.

Una vez conocidos esos indicadores, podemos procesar las frases y conocer la repercusión en la tasa de acierto de palabras (calidad del sistema) y poder establecer una cierta correlación “tanto por ciento del espacio óptimo procesado – degradación del sistema”, lógicamente al aplicar un umbral estimado en base a ese histograma. Esta correlación podrá encontrarse en los resultados y gráficas incluidas en el apartado de experimentación al final de esta capítulo.

Anterior   I  Siguiente   I  Índice capítulo 5   I  Índice General