5.3.2.1 Recorte basado en un Ancho de Haz Constante

La estrategia del Recorte basado en un Ancho de Haz Constante consiste en calcular un parámetro, trama a trama, y sumarle una constante (el ancho del haz) igual para todas las tramas, de modo que se establezca una franja de distancias activas (en lugar de distancias podrían ser probabilidades, pero en esta tesis, se trabaja siempre con distancias).

El parámetro es la distancia del mejor estado de todo el espacio de búsqueda en esa trama, es decir, el estado de menor distancia acumulada. No se puede asegurar que el mejor de los estados pertenezca siempre al camino óptimo pero se ha comprobado que está muy cerca. Por tanto, al sumar una constante al parámetro calculamos un umbral de distancias, dando lugar a una franja de distancias comprendida entre el parámetro y dicho umbral. El umbral de distancia debe asegurar que la distancia del estado del camino óptimo en esa trama se encuentra por debajo de él, es decir, dentro de los límites de la franja. Todos los estados del espacio de búsqueda cuyas distancias se encuentren en esa franja (por debajo del umbral) se considerarán estados activos para la siguiente trama, siendo candidatos a procesar en la trama siguiente junto a los estados que puedan seguirle teniendo en cuenta las restricciones impuestas por las topologías gramatical y acústica (HMM). El método parece sencillo de aplicar pero adolece, desde nuestro punto de vista, de varios problemas:

• La determinación de la constante a sumar, en cada trama, al parámetro calculado. No se conoce ningún método que intente formalizar el problema de la búsqueda a priori del mismo. Ello es debido, en parte, al desconocimiento, a priori, del comportamiento del espacio de búsqueda a lo largo del proceso de reconocimiento. En la mayoría de los casos la determinación de la constante a sumar se realiza de forma experimental, comprobando sobre un conjunto de datos de prueba, cómo afectan los distintos valores de esta constante en la Tasa de Aciertos de Palabras (WA) del sistema. De ese modo se elige un valor para la constante que, reduciendo al máximo posible el tamaño del espacio de b´suqueda a procesar en cada trama, mantenga la degradación de la Tasa de Aciertos de Palabras dentro de unos valores razonables.
• El incremento de cálculo que supone estimar el espacio de búsqueda activo para la siguiente trama basándonos en lo procesado en la trama actual. A veces, este incremento es tal que la reducción de estados a procesar se compensa con el aumento de proceso debido al cálculo del propio espacio para la siguiente trama. Debido a que es necesario recorrer todo el espacio de búsqueda actual y comparar la distancia de cada estado del espacio de búsqueda activo con el umbral, decidiendo cuáles van a ser eliminados y cuáles no.
• La única adaptación que tiene el umbral calculado al espacio de búsqueda activo es el parámetro calculado, que varía de trama a trama. Sin embargo, no tiene en cuenta la distribución de las distancias de los estados del espacio de búsqueda activo con respecto al parámetro en cada trama. Se ha comprobado que esta distribución varía, existiendo tramas en las que, debido a esa distribución, el ancho del haz podría disminuir mientras que en otras (de mayor confusabilidad) debería aumentar. La técnica que tiene en cuenta esa distribución de distancias trama a trama se conoce como Recorte basado en un Histograma de Estados y parece conseguir mejores resultados (al variar el ancho del haz de búsqueda) aunque es más costosa computacionalmente que la que hemos implementado [NEY92]. También podríamos llamar a esta nueva técnica como Recorte basado en un Ancho de Haz Variable, en contraposición con el nombre de la técnica utilizada en esta tesis.

Para comprender mejor cómo funciona esta técnica de recorte hemos representado en las gráficas 5.9 y 5.10 detalles del espacio de búsqueda en función de un umbral de recorte

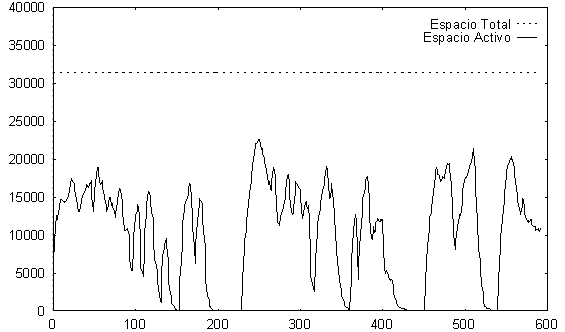
En la gráfica 5.9 se observa el espacio de estados activo a lo largo de las tramas de una frase al aplicar la técnica de recorte que estamos comentando. En ella también podemos ver el espacio de estados total que habría que procesar si no aplicamos ninguna técnica de recorte. Es fácil comprobar cómo el espacio de búsqueda activo varía a lo largo de las tramas. Ello se debe a la existencia de zonas donde el umbral de recorte no puede eliminar tantos estados al existir un índice de confusabilidad mayor y existir, por tanto, un mayor número de estados con distancias acumuladas muy cercanas.

Fig. 5.9 Espacio de Estados Activo vs. Espacio de Estados Total para una frase (ST0023) usando el método del Recorte basado en un Ancho de Haz Constante con 2 umbrales. Espacio Activo Medio 33.5 %

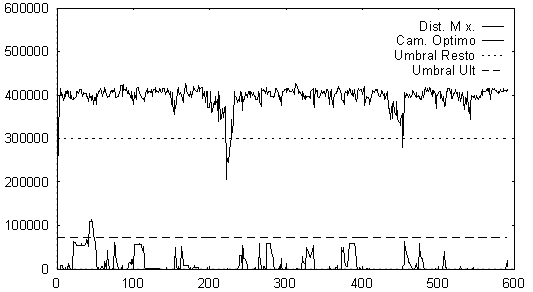
En la gráfica 5.10 podemos ver la evolución de la distancia máxima y la distancia  de los estados del camino óptimo  a lo largo de las tramas de una frase. Las curvas representan las diferencias entre dichas distancias y la distancia del estado de menor distancia en cada trama (parámetro). Es interesante destacar el margen tan amplio que existe entre ambas curvas de distancia y cómo un umbral de recorte divide esa franja en dos zonas, siendo crucial que la zona comprendida entre el eje x y el umbral (o umbrales) no corte excesivamente la curva de la distancia de los estados del camino óptimo de esa frase (curva inferior).

inferior).

Fig. 5.10 Evolución de la distancia máxima y la distancia de los estados del camino óptimo a lo largo de las tramas de una frase, con relación a la distancia mínima en cada trama. También se muestran los umbrales para los últimos estados y los no últimos de un modelo HMM. Se ha empleado el método del Recorte basado en un Ancho de Haz Constante con dos umbrales, manteniendo un 99.0 % (factor de conservación) de los estados del camino óptimo de esas frase.

También se ha estudiado el comportamiento de la función distancia acumulada para los distintos estados del modelo de Markov de una palabra, detectando una cierta diferencia entre el último estado del modelo y el resto de los estados. La distancia, en cada trama, para los últimos estados de los modelos de Markov de palabra, parece concentrarse más en torno al valor de distancia del parámetro calculado que la distancia del resto de los estados del modelo. Por tanto, se han realizado experimentos utilizando uno y dos umbrales de recorte, evaluando la posibilidad de ajustar el recorte de caminos de forma independiente para los últimos estados de un modelo HMM que para el resto de los estados.

Además, se han realizado experimentos para comprobar el efecto de una gramática y de un mejor modelado (modelos semicontinuos de Markov) en el propio proceso de recorte.

Anterior   I  Siguiente   I  Índice capítulo 5   I  Índice General