5.1.3 Suavizado de la Gramática MC160 usando la técnica Back-Off

La falta de suficientes datos de entrenamiento produce que la matriz cuadrada de 160 macrocategorías contenga muchos ceros de probabilidad, es decir, pares de macrocategorías que no han sido observadas en esos datos. El problema derivado de ello es la falta de cobertura de la gramática, que puede lugar a errores en el sistema de reconocimiento cuando la gramática guía dicho proceso, no permitiendo frases no observadas en el entrenamiento pero que pueden ocurrir con cierta facilidad en el conjunto de datos de prueba (o en el funcionamiento real del sistema en una aplicación). Ya comentamos que para evitar ese tipo de errores se lleva a cabo un proceso de suavizado o “rellenado” de la matriz de la gramática, sustituyendo los ceros de probabilidad por valores adecuados, calculados mediante una técnica conocida como back-off [KAT87]. Esta técnica es una de las más utilizadas pues tiene un coste computacional razonable y ha demostrado ser muy útil para conseguir modelos lingüísticos estadísticos robustos. Esta técnica propuesta por Katz está basada en la fórmula de Turing-Good [GOO53].

A continuación se muestra la expresión matemática (fórmula) utilizada para calcular las probabilidades de los elementos de la matriz, que nuestro caso son pares de macrocategorías del conjunto de 160 macrocategorías definidas en el Proyecto 860, de donde ya hemos dicho hemos obtenido los datos originales.

[Fórmula]

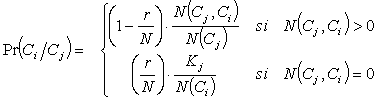
Fig. 5.5 Ecuaciones de cálculo de las probabilidades de los elementos de la matriz utilizando el método “back-off”

La definición de cada elemento de la fórmula utilizada se incluye a continuación, para facilitar la comprensión de la misma.

[Definiciones] r : Número de pares de categorías diferentes que sólo se han dado una vez en el entrenamiento, es decir, para las que : Frecuencia de aparición en el entrenamiento de Cj N : Número total de bigramas del conjunto de entrenamiento : Frecuencia de aparición en el conjunto de entrenamiento del par CjCi : Frecuencia de aparición en el conjunto de entrenamiento de Ci : Probabilidad de que un par de categorías no se haya visto en el entrenamiento Kj : Constante de normalización. Su objetivo es conseguir que

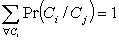
Fig. 5.6 Definiciones relacionadas con las ecuaciones de la figura 5.5

Es importante aclarar que el suavizado de la matriz gramatical conduce a un empeoramiento de la perplejidad del modelo lingüístico, ya que ahora muchas restricciones han desaparecido. El aumento de la cobertura de la gramática supone un aumento de la perplejidad, que se espera que no conduzca a un empeoramiento de la tasa de error del sistema excesivo.

En las ecuaciones de la figura 5.5 se muestra como la probabilidad de un bigrama Pr(C_i / C_j) se calcula mediante la combinación de dos componentes: una función descuento y una función de redistribución. La primera de las funciones está relacionada con el problema de la estimación de la probabilidad de frecuencia-cero (en nuestro caso es r / N), es decir, la probabilidad de todas aquellos bigramas que nunca han ocurrido en el conjunto de entrenamiento. La segunda función se encarga de redistribuir la probabilidad de frecuencia-cero (r / N) entre los bigramas no observados, de acuerdo con el modelo de orden menor (en nuestro caso, un unigrama, es decir, Pr(C_i) = 1 / N(C_i)).

Existen varios métodos para el cálculo de la función descuento y la función de distribución. Entre los más conocidos se encuentran: Suma-1 (Adding-1), la fórmula de Good-Turing, Descuento Absoluto (Absolute or Shift Discounting), Descuento Lineal (Linear Discounting). En nuestro caso hemos optado por el método del Descuento Lineal y concretamente por el Descuento Lineal Simple, que utiliza una constante de descuento que puede ser estimada asumiendo que el hecho de aparición de nuevas palabras después de un determinado contexto es un proceso de Poisson, de donde se obtiene la constante r / N que ya comentamos [FED95].

Anterior   I  Siguiente   I  Índice capítulo 5   I   Índice General